Some interesting properties of Manhattan geometry

Manhattan geometry, which is a discrete geometry whose axioms are:

• the universe is discretized in quantum of distance;
• 2 points A & B defines more than one segments;
• a circle is twitesd square, but a square is still a square;
• something about the sum of the angle in a triangle;
• there is an infinite number of rights coming through a point, but it is an infinity less than in euclidean geometry;
• parallels may share an infinity of subsegment that are periodics;
• the generalized distance is L1 for whatever dimension you use;

Note

Given:

• dimension varying from 0 to i;
• X,Y denoting of coordinate Union(| xi >) Union(| yi >)

Then distance is : D(x,y)=Sum(0,i)(abs(yi-xi))

For the following let us denote C(O,r,x) a circle C of center O(irigin) with a radius r, with a level of discretization x. Default being 1.

The level of discretization indicates how many division I accept in the unit vector.

Circonference of a circle

Note

Circonference(C(O,r,d)=8 x r

Whatever the discretization level is Circonference will always be the same o/

Area of circle

This one is quite funnier, so let’es draw some pictures :)

The area is measured by the number of square contained within the envelope of a Circle C(O,r,d) such as any edge is a vertex which length is inferior or equal to r measured by L1 from O.

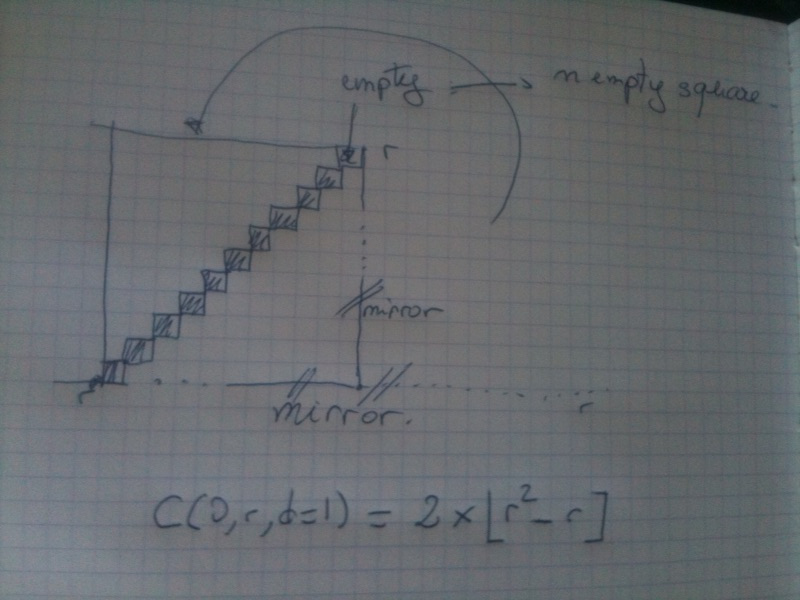
Which strangealy enough tells us that the area of C(0,1,1) is 0

Now let’s study the case where the discretization level is not 1 for unit Circle: C(O,1,d=x).

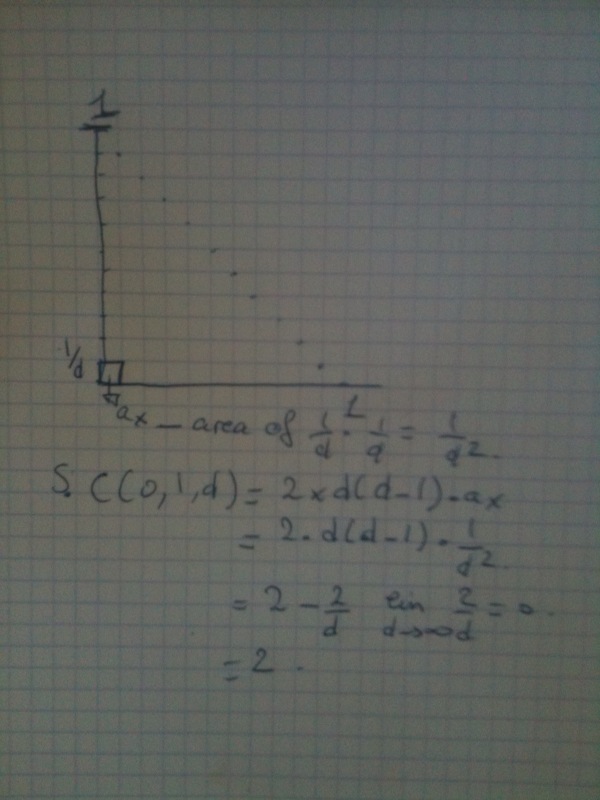
Note

The surface of the unit circle will tend towards 2. A(0,1,d)=2(1-1/d)

It is trivial to demonstrate that A(0,r,d=D)=r.(A(0,1d=D) thus

Note

A(0,r,d)=r.2.(1-1/d)

A(0,r,d=>inf)=2xr

Nth dimensional probem of the volume

This one is boring easy so let’s just state the results:

Note

given n dimension, the volume V of dimemsion n is

Vn(0,r,d=>inf)=2^(n-1) . r

Plus if the Area of dimension n is denoted A

An(0,r,d) > Vn(0nr,d) whatever the dimension is

So in three dimensions for instance, the surface of the sphere will have a measure in measure^n inferior to its surface in measure^(n-1), thus the ratio V/A < 1. In a Manhattan driven geometry big mammals would not exists, since the reason to be of large mass is diminishing this ratio so that you radiate less heat.

Since computers are Manhattan driven geometry, thus some problem might give false results.

Conclusion

Geometry are abstract yet intuitive constructions. What may looks like an intellectual wanking is interesting: Manhattan geometry is a geometry fitted for problems where distance between to points can be expressed as quantum of differences. Plus since it is pretty intuitive, it is easier to handle than nth dimension generalized euclidian geometry.

Plus since is does not rely on real numbers but on on natural integers, measures are peculiarly well suited for computers. Since we have order relations it permits what we love to do with computers:

• comparing;
• sorting.